# 9.树和二叉树:如何实现增删改查
# 9-1 树是什么
树是由结点和边组成的,不存在环的一种数据结构
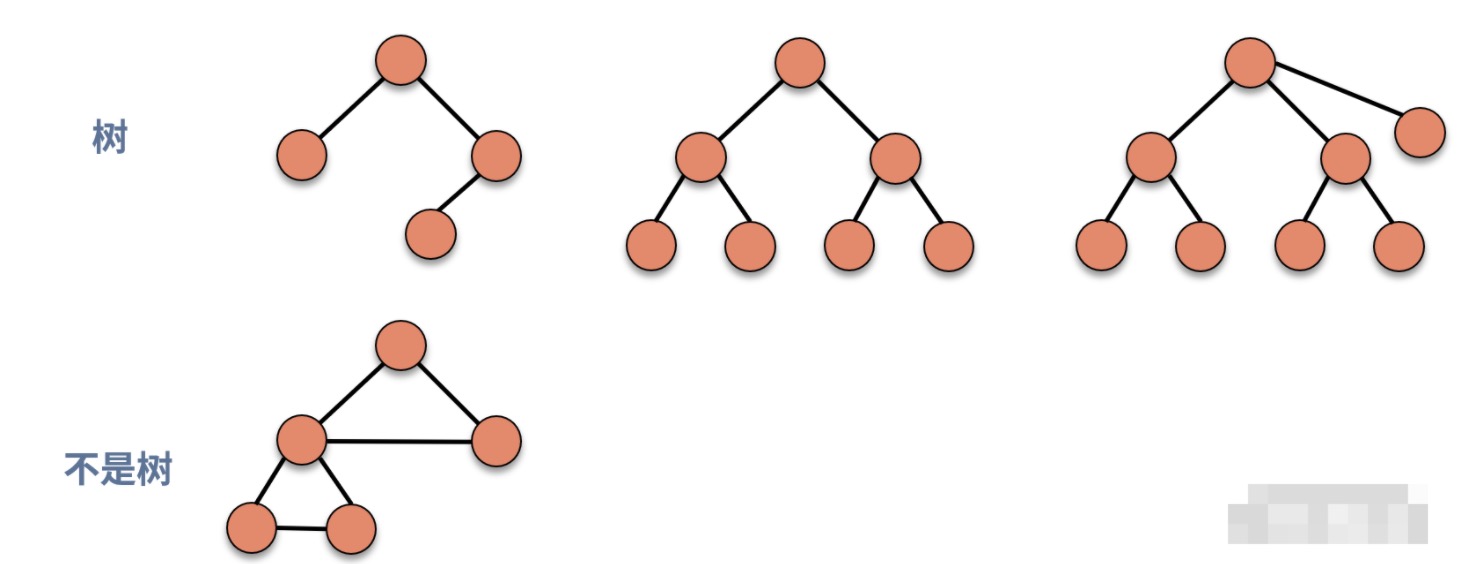
树满足递归定义的特性,也就是说,如果一个数据结构是树,那么剔除根结点后,得到的若干子结构也是树,通常称为子树
- A结点是B结点和C结点的上级,则A就是B和C的父结点,B和C是A的子结点
- B和C 同时是A的‘孩子’,则可称为B和C互为兄弟结点
- A没有父结点,则A被称为根结点
- G、H、I、F结点都没有子结点,则称G、H、I、F为叶子结点
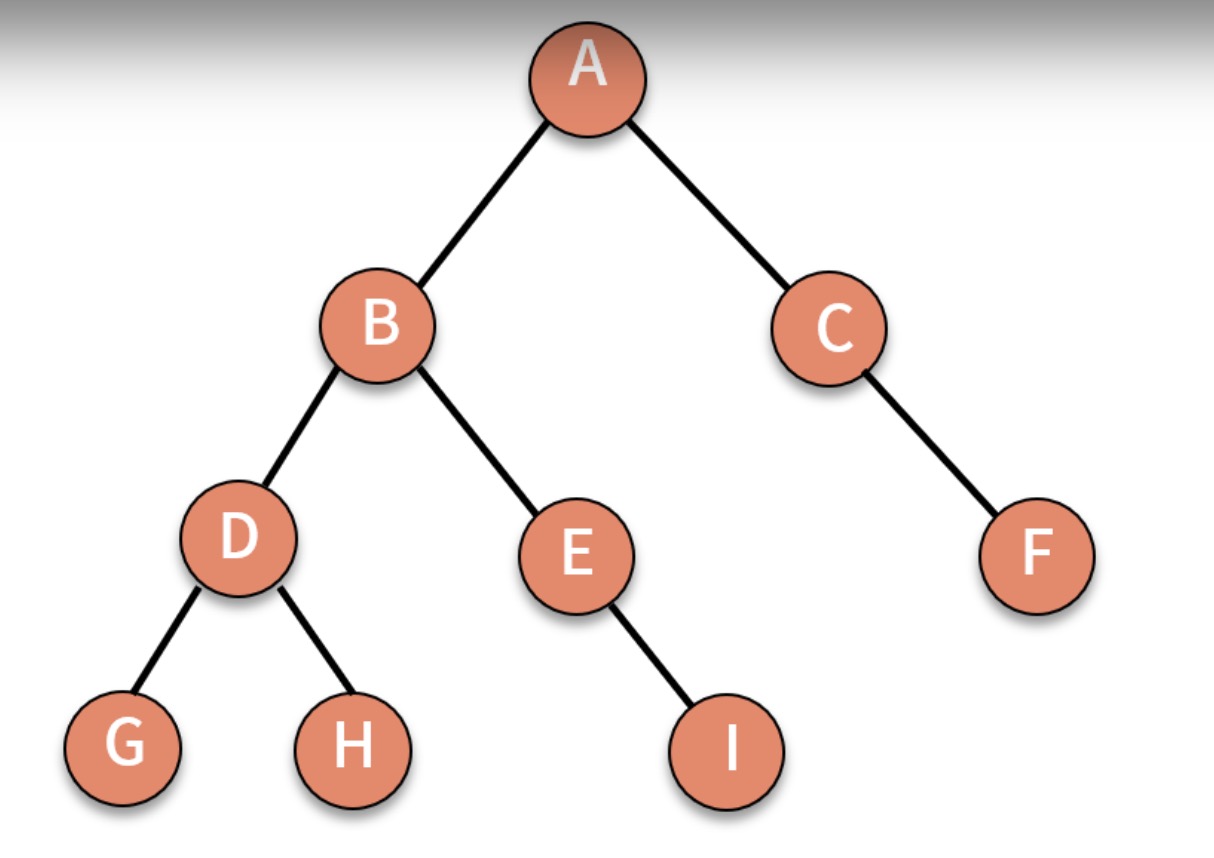
但有了一颗树,还需要用深度、层来描述这棵树中结点的位置。结点的层级从根结点算起,根为第一层,根的‘孩子’为第二层,根的‘孩子’的‘孩子’为第三层,依次类推,树中结点最大层次数,就是这棵树的树深(称为深度也称为高度),如上图所示,这就是一颗深度为4的树
# 9-2 二叉树是什么
在树的大家族中,有一种被高频使用的特殊树,这种就是二叉树。在二叉树中,每个结点最多有两个分支,即每个结点最多两个子结点,分别称为左子结点,右子结点。在二叉树中,有,两个特殊的类型
- 满二叉树,定义为除了叶子结点外,所有结点都有2个子结点
- 完全二叉树,定义为,除了最后一层以外,其他层的结点个数都达到最大,并且最后一层的叶子结点都靠左排列

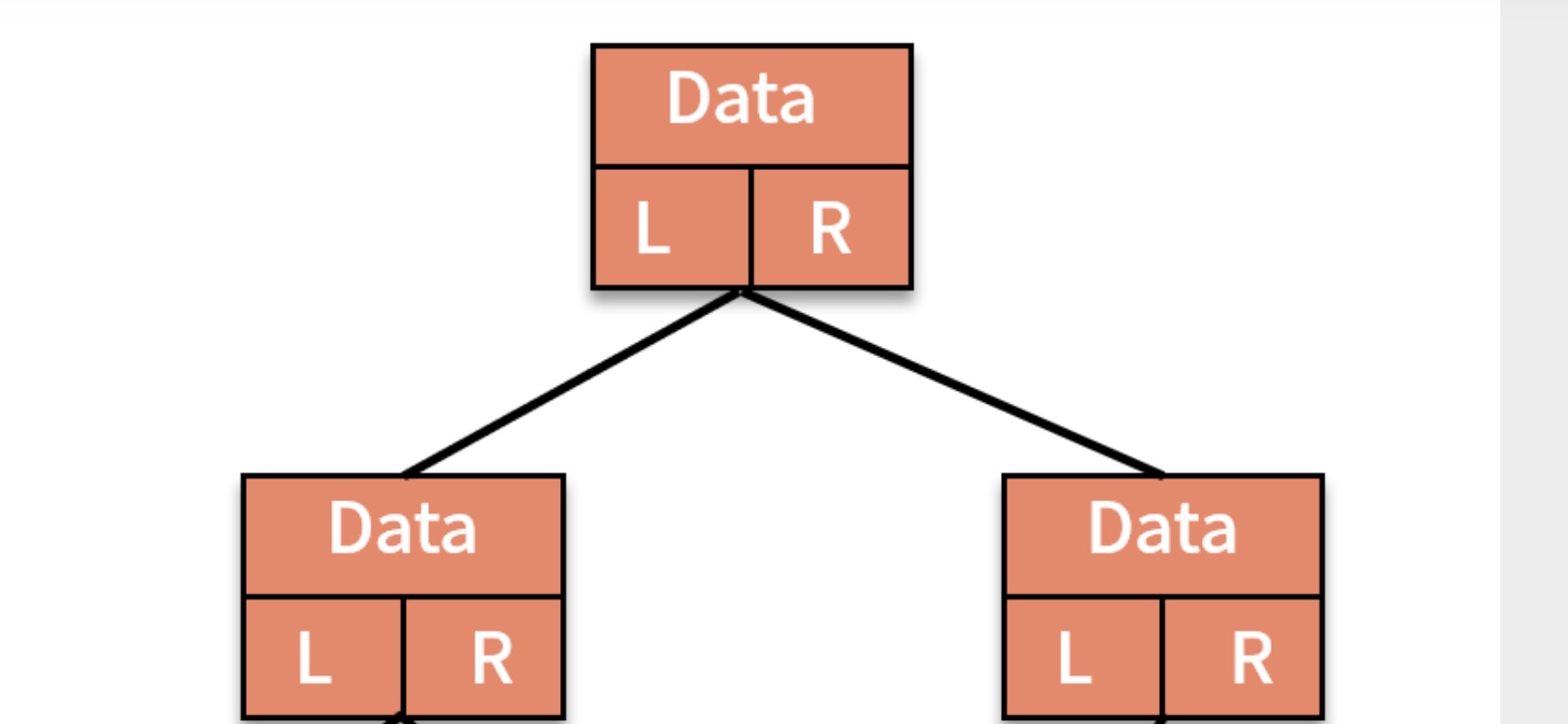
为什么完全二叉树看起来并不完全,还这样称呼?这个和二长树的存储有关,存储二叉树有两种办法,一种是指针的链式储存,一种是分别存放指向左右子结点的指针:
- 链式存储法,也就是像链表一样,每个结点有三个字段,一个存储数据,另外两个分别存放指向左右子结点的指针,如图:
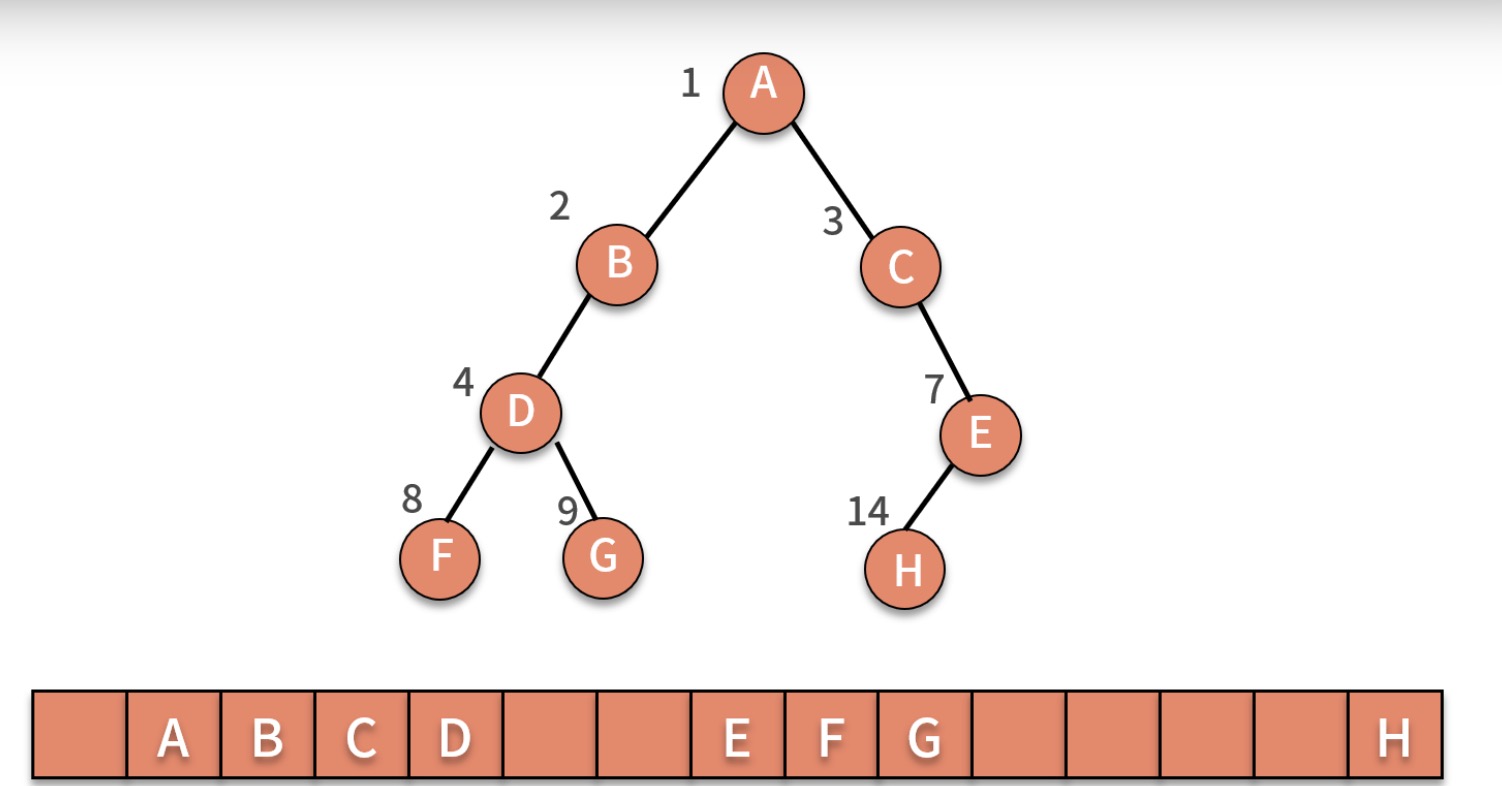
- 顺序存储法,就是按照规律把结点存放在数组里,为了方便计算,我们会把根结点放在位置1的地方,随后,B结点存放在下标为2的位置,C放到3的位置,以此类推,就会发现规律:X的下标为i,X左侧的结点就是2i,X右子结点总是存放在2i+1的位置
之所以称为完全二叉树,是从存储空间利用效率视角来看的,对于一颗完全二叉树而言,仅仅浪费了下标为0的存储位置。而如果是一颗非完全二叉树,则会浪费大量储存空间。
如下图所示,它既需要保留5和6的位置,同时也需要保留5的两个子结点10和11的位置,以及6的两个子结点12和13的位置,没有完全利用好数组的存储空间
# 9-3 树的基本操作
链表、栈、队列都是‘一对一’的关系,但树是‘一对多’的关系
在‘一对一’对结构总,直接顺序访问,在‘一对多’的关系,我们要怎么去遍历并保证没有遗漏
其实遍历一棵树,有经典三种方法,分别是前序遍历、中序遍历、后序遍历。这里的序指的是父结点的遍历顺序,前序就是先遍历父结点,中序就是中间遍历父结点,后序就是最后遍历父结点。不管哪种遍历,都是通过递归完成的。
- 前序遍历,对树中的任意结点来说,先打印这个结点,然后前序遍历它的左子树,最后前序遍历它的右子树
- 中序遍历,对树中的任意结点来说,先中序遍历它的左子树,然后打印这个结点,最后中序遍历它的右子树
- 后序遍历,对树中的任意结点来说,先后序遍历它的左子树,然后后序遍历它的右子树,最后打印它本身
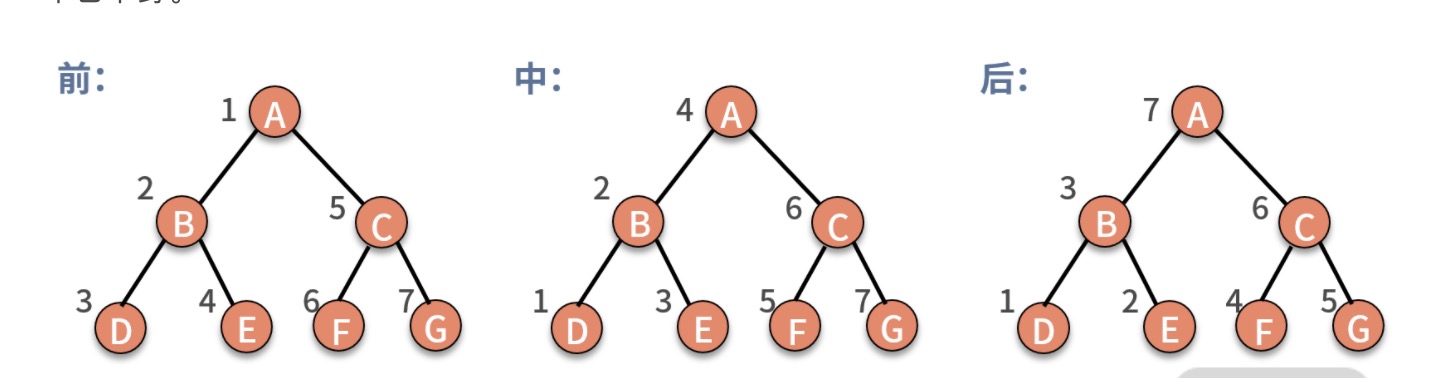
下面用代码来实现遍历过程
//先序排列
function preOrderTraverse(node){
if(node == null){
return
}
Document.write(node.data + ' ');
preOrderTraverse(node.left);
preOrderTraverse(node.right)
}
//中序排列
function inOrderTraverse(node){
if(node == null){
return
}
inOrderTraverse(node.left);
Document.write(node.data + ' ');
inOrderTraverse(node.right);
}
//后序排列
function postOrderTraverse(node){
if(node == null){
return
}
postOrderTraverse(node.left);
postOrderTraverse(node.right);
Document.write(node.data + ' ');
}
不难发现,每个结点都被访问了一次,所以其时间复杂度为O(n);
找到位置之后执行删除操作,我们需要通过指针建立连接关系就可以了。
对于没有任何特殊性质的二叉树而言,抛开遍历的时间复杂度,真正执行增加删除操作的时间复杂度为O(1)
树数据的查找操作和链表一样,都需要遍历数据去判断,所以时间复杂度为O(n)
# 9-3-1 二叉查找树的特性
二叉查找树(也称作二叉搜索树)具备以下几个特性
- 在二叉查找树中的任意一个结点,其左子树中的每个结点的值,都要小于这个结点的值
- 在二叉查找树中的任意一个结点,其右子树中每个结点的值,都要大于这个结点的值
- 在二叉查找树中,会尽可能规避两个结点树值相等的情况
- 对二叉查找树进行总序遍历,就可以输出一个从小到大的有序数据队列,中序遍历
# 9-3-2 二叉查找树的查找操作
在利用二叉查找树执行查找操作时,我们可以进行以下判断
- 首先判断根结点是否等于要查找的数据,如果是就返回
- 如果根结点大于要查找的数据,就在左树中递归执行查找动作,直到叶子结点
- 如果根结点小于要查找的数据,就在右子树中递归执行查找动作,直到叶子结点
这样的‘二分查找’所消耗的时间复杂度就可以降低为O(logn)
# 9-3-3 二叉查找树的插入操作
二叉树的插入,从根结点开始,如果插入数据比根结点大,且根结点的右子结点不为空,则根结点的右子树中继续尝试插入操作,直到找到为空的子结点执行插入操作。
例如,要插入数据X的值为14,则需要判断X与根结点的大小关系
- 由于14小于16,则聚焦在左子树,继续判断X与13的关系
- 14大于13,则聚焦在右子树,继续判断X与15的关系
- 由于14小于15,则聚焦在其左子树
- 此时左子树为空,则直接通过指针建立15结点的左指针指向结点X的关系,就完成插入动作
二叉查找树插入数据的时间消耗是O(logn),这并不意味它比普通二叉树要复杂,原因在于这里的时间复杂度更多是消耗了在遍历数据去找到查找位置,真正执行插入动作的时间复杂度仍然是O(1)
# 9-3-3 二叉查找树的删除操作
二叉查找树的删除操作比较复杂,因为删除完某个结点后的树,仍然要满足二叉查找树的性质,会有以下三个情况:
- 情况一,如果要删除的是某个叶子结点,则直接删除,将其父结点指针指向null即可
- 情况二,如果删除的结点只有一个子结点,只需要将其父结点指向的子结点指针换成其子结点的指针即可
- 情况三,如果删除的结点有两个子结点,则两种可行的操作方法
第一种,找到这个结点的左子树中最大的结点,替换要删除的结点
第二种,找到这个结点的右子树中最小的结点,替换要删除的结点
# 9-4 树的案例
输入一个字符串,判断它已有的字符串集合是否出现过?已有字符串集合包含6个字符串,分别为:cat,car,city,dog,door,deep;输入cat,输出true,输入home,输出false
我们采用 暴力方法,估算一下时间复杂度,假设字符串包含了n个字符串,其中的字符串平常长度为m,新来一个字符串,需要与每个字符串进行匹配,则时间复杂度为O(nm);
在nm复杂度中,显然存在很多无效匹配;因此,如果通过对字符前缀进行处理,就可以最大限度地减少无谓的字符串比较,从而提高查询效率。就是‘用空间换时间’的思想,再利用共同前缀提高查询效率
这个问题也可以用树结构完成;我们对字符串建立一个树的结构,它将字符串集合的前缀进行合并,每个结点到叶子结点的链条就是一个字符串,这个树结构也称作Trie树,或字典树,有三个特点
- 第一,根结点不包含字符
- 第二,除根结点以外,每个结点都只包含一个字符
- 第三,从根结点到某一个叶子结点,路径经过的字符连接起来,即为集合中的某个字符串
这个问题的解法可以拆成两个步骤
- 第一步:根据候选字符串集合,建立字段树,这需要使用数据插入的动作
- 第二步:对于一个输入字符串,判断它能否在这个树结构中走到叶子结点,如果能则出现过
# 9-5 总结
- 熟悉二叉树的三种遍历方式,遍历的时间复杂度为O(n),遍历之后,就可以在指定位置的数据增删操作,增删操作时间复杂度为O(1)
- 查找操作,普通二叉树,查找时间复杂度和遍历一样都是O(n);如果是二叉查找树,则需要在O(logn)时间复杂度完成查找;树结构在存在‘一对多’的数据关系中,可被高频使用,这也是它区别于链表系列数据结构的关键点